Estimates of measurement uncertainty associated with Clinical Laboratories and their implications for clinical practice

 

José Robson Venturim¹, Luiza Valli Vieira²

 

¹  Grupo Tommasi Laboratórios, Diretor Técnico, Farmacêutico-Bioquímico; Especialista em Análises Clínicas e Mestre em Patologia Geral das Doenças Infecciosas.

²  Grupo Tommasi Laboratórios, Coordenadora/Responsável Técnica Cromatografia, Doutora em Química.

 

Recebido em 01/11/2024

Aprovado em 15/11/2024

DOI: 10.21877/2448-3877.202400216.pt

 

INTRODUÇÃO

Uma medição é um ato de estabelecer um valor numérico a uma grandeza específica, através de algum processo de experimentação.⁽¹⁾ Nesse processo, o valor encontrado (ou seja, o resultado) é dado com base em uma comparação com um padrão conhecido, sendo, portanto, uma estimativa. Entretanto, é preciso entender que toda medição apresenta um componente denominado “incerteza de medição”, que é parte integrante do valor apresentado como resultado da medição. É importante ressaltar que incerteza de medição é diferente de erro de medição (EM), definido como a “diferença entre o valor obtido e o valor verdadeiro, quando este for disponível”.⁽¹⁾

A incerteza de medição (MU, do inglês measurement uncertainty) é um parâmetro que quantifica a dúvida associada ao resultado de uma medição. Por definição, o VIM (Vocabulário Internacional de Metrologia) define a incerteza de medição como “o parâmetro não negativo que caracteriza a dispersão dos valores atribuídos a um mensurando, com base nas informações utilizadas”.⁽¹⁾ Em outras palavras, a MU indica a faixa dentro da qual o valor verdadeiro da medição provavelmente se encontra, uma vez que, como não se trata de um parâmetro negativo ou nulo, sempre haverá um conjunto de incertezas (Incerteza expandida, designada por “U”) associada ao valor quantitativo do mensurando.⁽²⁾ A MU é uma estimativa que quantifica a confiabilidade dos resultados de uma medição, de forma que quanto maior a incerteza, menor a confiabilidade do resultado.⁽³⁾

A informação obtida através do processo de medição permite atribuir ao mensurando apenas um “intervalo de valores razoáveis”. Informações adicionais relevantes podem reduzir a amplitude desse intervalo (diminuindo a incerteza) que pode ser atribuído ao mensurando. No entanto, mesmo a medição mais precisa não é capaz de reduzir o intervalo a um único valor, em razão da quantidade finita de detalhes na definição do mensurando.⁽¹⁾

O resultado de uma medição é composto pelo resultado-base (RB) e a faixa (range) formada pela MU, para mais e para menos. O valor verdadeiro está contido dentro desta faixa, sendo, idealmente, o mais próximo possível do ponto central, onde está o RB, ou seja, quanto menor for a MU mais próximos estarão o valor verdadeiro e o RB.⁽¹⁾

A Figura 1 ilustra a disposição de um resultado obtido em uma medição (resultado-base, ou RB), o valor verdadeiro e a amplitude de possíveis valores em torno do RB, considerando a MU.

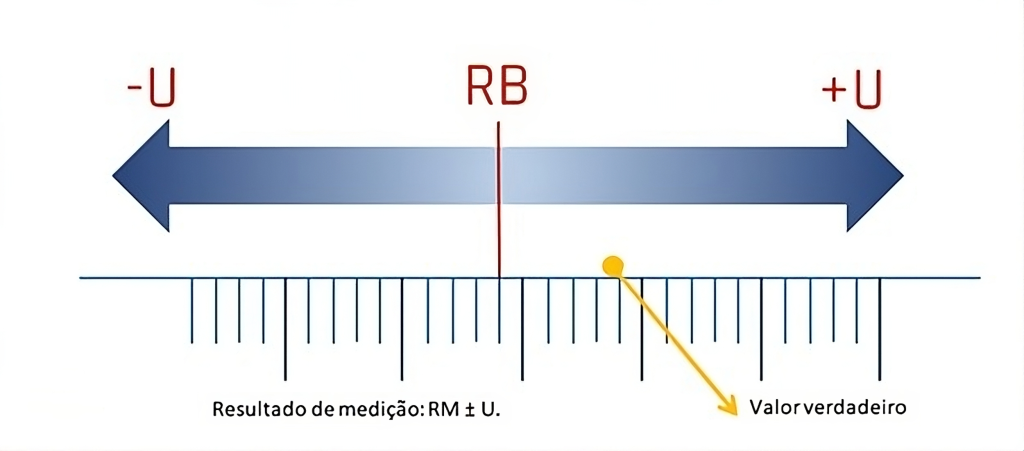
Figura 1

Demonstração da distribuição dos componentes de uma medição.

Legenda: RB, resultado-base; U, incerteza expandida; RM, resultado da medição. Fonte: ACC, 2024.⁽⁴⁾

 

A incerteza é um conceito estatístico que reflete os efeitos de diversos fatores que surgem durante os processos de medição, impactando os resultados obtidos.⁽⁵⁾ Segundo a Diretriz CLSI EP29-A (Clinical and Laboratory Standards Institute)⁽⁵⁾ , a incerteza define um intervalo no qual se espera que o valor real da medição esteja com um nível de confiança especificado. Na prática dos processos de medição e avaliação do desempenho analítico existem três tipos principais de incerteza: padrão, combinada e expandida.⁽⁵⁾

A incerteza padrão refere-se à imprecisão determinada em laboratório, ao passo que a incerteza combinada associa outras possíveis fontes e a incerteza expandida leva em consideração o intervalo de confiança desejado para a aplicação da medição. Avaliar a incerteza de medição dos resultados laboratoriais é crucial para verificar o desempenho do sistema de medição. A incerteza proporciona aos profissionais de laboratório uma compreensão mais profunda do desempenho e das limitações de seus métodos, permitindo a identificação de etapas técnicas nas quais a incerteza pode ser potencialmente reduzida. Para a segurança dos pacientes, é essencial que a maioria dos exames laboratoriais esteja dentro da meta analítica de seu uso clínico, pois isso pode influenciar significativamente a capacidade do clínico de avaliar corretamente os pacientes.⁽⁵⁾

A incerteza pode surgir de várias fontes, como de instrumentos de medição, envolvendo suas limitações e precisão dos dispositivos utilizados, nível de automatização dos equipamentos e padronização de métodos analíticos comerciais em contraposição a metodologias desenvolvidas e validadas no próprio laboratório; condições ambientais, como variações de temperatura, umidade etc.; métodos de medição, como os procedimentos, metodologias, protocolos e técnicas; diferenças individuais do operador, como habilidade e experiência da pessoa que realiza a medição, sobretudo em metodologias não automatizadas.⁽⁶⁾

Compreender e especificar a incerteza é crucial para garantir a confiabilidade e a comparabilidade dos resultados, especialmente em áreas como laboratórios clínicos, onde decisões importantes são baseadas nesses dados.⁽⁵⁾ A Figura 2 fornece uma visão em formato de diagrama de causa e efeito, do tipo “espinha de peixe”, exemplificando uma situação hipotética na qual as fontes de incertezas, de uma medição laboratorial, fossem estudadas.

 

 

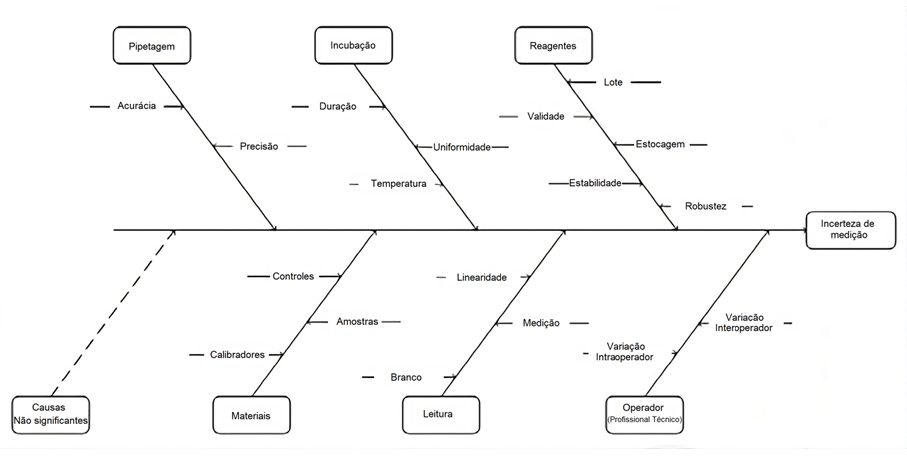
Figura 2

Demonstração esquemática da identificação das fontes de incertezas visando a determinação da incerteza de medição (MU) de um exame laboratorial.

Fonte: Pereira, 2016.⁽⁶⁾

 

Estimar e quantificar a incerteza nas medições é crucial para os laboratórios clínicos por várias razões, sendo as principais as características de precisão e confiabilidade. A incerteza ajuda a determinar a precisão e a confiabilidade dos resultados dos exames laboratoriais, sendo essencial, portanto, para garantir que os diagnósticos e tratamentos baseados nesses resultados sejam corretos, pelas inferências clínicas atribuídas a esses resultados laboratoriais, influenciando diretamente em tomadas de decisão clínica.⁽⁷⁾ Além disso, outro requisito importante, uma vez determinadas as incertezas de medição e apresentadas junto aos resultados, é a comparabilidade, pois permite a comparação de resultados entre diferentes laboratórios e métodos analíticos. Sem uma estimativa de incerteza, seria difícil saber se as diferenças nos resultados são significativas ou apenas variações normais. Para adequação aos padrões de qualidade para atendimento de normas e legislações, a especificação da incerteza é um requisito de normas internacionais, como a ISO 15189-2012, ou mesmo normas nacionais como a 8ª edição do Manual do Sistema Nacional de Acreditação do Departamento de Inspeção e Credenciamento da Qualidade (SNA/DICQ) da Sociedade Brasileira de Análises Clínicas (SBAC), em seu item 5.5.1.4, sendo que cumprir esses padrões é fundamental para a acreditação e reconhecimento dos laboratórios clínicos.⁽⁷⁾

A história do controle da qualidade em análises clínicas, especialmente na bioquímica clínica, é extensa e rica. Fundamentalmente, existem dois aspectos principais que são monitorados de forma rotineira: imprecisão, também conhecida como erro aleatório, e a inexatidão, também chamado viés, bias ou erro sistemático dos resultados. A sistemática de controle interno da qualidade (CIQ) é essencialmente voltada para avaliar a imprecisão, enquanto o controle externo da qualidade (CEQ), sobretudo os ensaios de proficiência (EP), tem como objetivo avaliar a inexatidão. A origem dos conceitos e aplicabilidade do CEQ remonta ao final da década de 1940, a partir da publicação de Belk e Sunderman.⁽⁸⁾ Por outro lado, o CIQ evoluiu gradualmente ao longo dos anos, especialmente a partir da década de 1970, quando Westgard, Groth e de Verdier introduziram simulações como uma ferramenta científica para avaliar e projetar regras de controle.⁽⁶⁾

O desempenho de um laboratório pode ser descrito de maneira satisfatória em termos de erros aleatórios e sistemáticos. A métrica conhecida como “erro total” (TE, do inglês total error), definida como o “efeito líquido do viés e da imprecisão do método”, incorpora ambos os tipos de erro.⁽⁹⁾ No entanto, uma objeção comum ao TE é que, se um viés conhecido está incluído, por que mantê-lo? Além disso, o viés possui um sinal, enquanto a imprecisão é uma característica de uma distribuição. Portanto, as quantidades incluídas no TE não são realmente comparáveis.⁽¹⁰⁾

 

Determinação das Incertezas de Medição

Planejamento da determinação da incerteza de medição

Tal qual a validação de métodos laboratoriais, antes de sua aplicação na prática laboratorial, a determinação da estimativa da incerteza de medição também requer um planejamento e uma sequência de avaliações.⁽⁶⁾ Métodos desenvolvidos em laboratórios de pesquisa e desenvolvimento (P&D), “in house” ou modificações muito extensas de métodos já validados necessitam de um processo de validação mais amplo e pormenorizado, diferentemente de métodos comerciais, validados por fabricantes e registrados em órgãos reguladores (ANVISA, FDA etc.).

No bojo do processo de validação analítica, vários dos processos necessários para a obtenção de dados utilizados na determinação da MU já serão realizados, sobretudo se a abordagem utilizada for a do tipo “bottom-up”, preconizada pelo guia para a expressão de incerteza de medição (GUM).⁽³⁾ No âmbito dos laboratórios clínicos, nos quais a maioria dos métodos utilizados já são padronizados, registrados e validados por fabricantes na forma de kits ou sistemas analíticos, as abordagens do tipo “top-down” têm sido mais aplicáveis, sobretudo considerando as limitações de informações a respeito do desenvolvimento dos métodos, por questão de patentes e restrições de segredo industrial, mas também pela dificuldade de obtenção de material de referência certificado (MRC) ou padrões de referência certificados (SRC).⁽¹¹⁾

Uma vez escolhida a estratégia e considerando as características do mensurando e do sistema analítico, o planejamento da determinação da MU consiste em:

• Descrição do mensurando, faixa (range) de medição, valor limite de MU.
• Identificar e quantificar os componentes de incertezas (Quantificar o componente de incerteza padrão para a reprodutibilidade intralaboratorial (u_Rw); Quantificar o componente de incerteza associado ao método e viés do laboratório (u_bias)).
• Converter as diferentes incertezas para valores de desvio-padrão do mensurando, por meio de suas variâncias.
• Determinar a incerteza padrão combinada (u_c), pela soma quadrática das incertezas padrão individuais.
• Calcular a incerteza expandida (U) considerando o fator estatístico de abrangência (k).

O fator k pode variar devido a alguns fatores, um dos principais é a precisão do item em mensuração, pois se o item não apresentar boa repetibilidade maior será a interferência no intervalo de confiança, aumentando o valor de k, o qual varia conforme os graus de liberdade efetivos adotados, conforme ilustrado na Figura 3.

 

Figura 3

Valores de k correspondentes aos graus de liberdade efetivos (Veff).

Fonte: ACC, 2024.⁽⁴⁾

 

O fator de abrangência k multiplica a incerteza padrão combinada para chegarmos a um nível de confiança de até 99,73% de abrangência, mas o mais utilizado é de 95,45%, ou seja, ± 2 DP, conforme ilustra a Figura 4, resultando na incerteza expandida (U) que corresponde à incerteza de medição (MU) aplicada ao valor obtido para o mensurando.⁽⁶⁾ Valores mais elevados de k implicam níveis de confiança mais elevados, entretanto também implicam a incorporação de valores com amplitude mais elevada e dados mais heterogêneos, com curvas mais achatadas e mais abertas, como ilustrado na Figura 5.

 

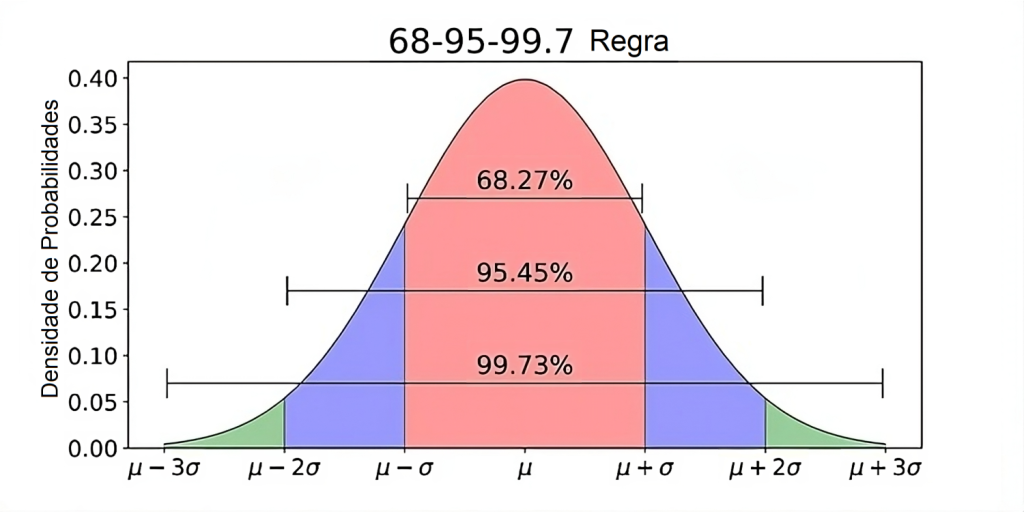
Figura 4

Distribuição estatística normal (binomial) “Gaussiana” descreve a função densidade de probabilidade, na qual a maior parte dos mensurandos em exames de laboratórios clínicos se distribui na faixa entre ±2 DP.

Fonte: Adaptado de https://towardsdatascience.com/understanding-the-68-95-99-7-rule-for-a-normal-distribution-b7b7cbf760c2.⁽¹²⁾

 

 

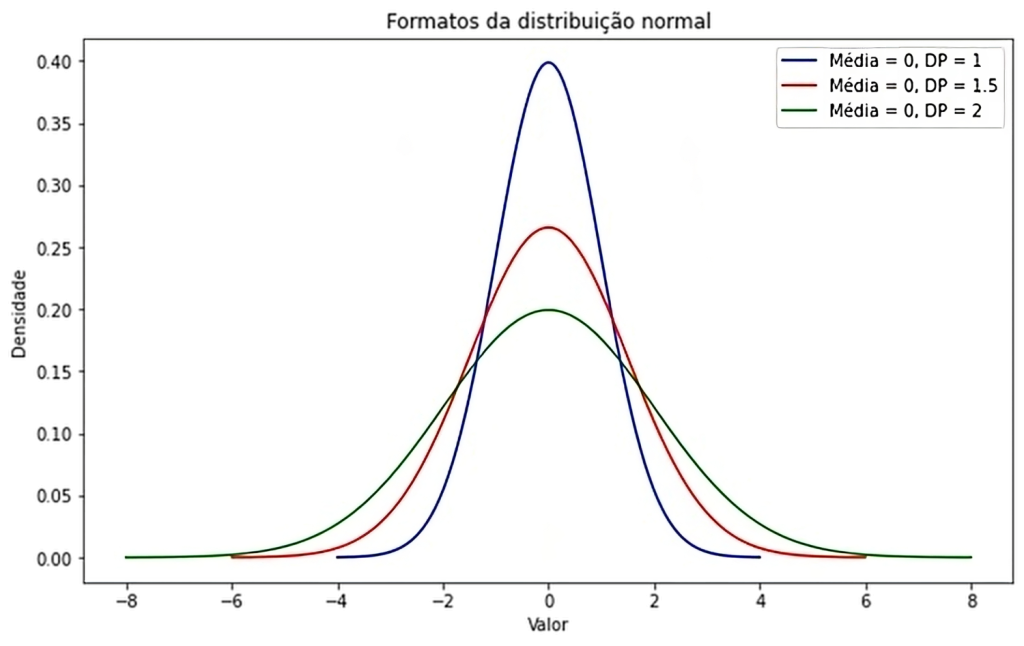
Figura 5

Ilustração da influência no aumento da variabilidade em relação ao valor de k. A linha mais elevada (azul) representa k = 2. As demais linhas representam valores acima de 2 para k.

Fonte: Adaptado de https://medium.com/data-hackers/desvendando-o-teorema-central-do-limite-17cbb13beb1a.⁽¹³⁾

 

Rastreabilidade metrológica

A rastreabilidade metrológica é definida como a “propriedade de um resultado de medição pela qual o resultado pode ser relacionado a uma referência por meio de uma cadeia ininterrupta documentada de calibrações, cada uma contribuindo para a incerteza da medição”.⁽¹⁾ Desta forma, a incerteza de medição deve ser metrologicamente rastreável, garantindo a comparabilidade dos resultados dentro de uma cadeia de rastreabilidade metrológica.⁽⁶⁾ Esta cadeia é definida como a “sequência de padrões de medição e calibrações utilizadas para relacionar um resultado de medição a uma referência”.⁽¹⁾ A Figura 6 ilustra um exemplo de cadeia metrológica para um exame de laboratório clínico. As incertezas e os vieses de medição são determinados conforme a cadeia de rastreabilidade metrológica. A precisão, o nível de acreditação do laboratório, a instabilidade e o custo por material aumentam significativamente dos laboratórios clínicos até o topo da hierarquia.⁽⁶⁾ De forma oposta, a incerteza de medição, o viés e a disponibilidade de materiais diminuem de baixo para cima.

Embora seja devidamente implementado na metrologia geral, não é amplamente empregado na maioria dos exames de laboratório clínico em razão da indisponibilidade de materiais de referência e métodos de referência. Além disso, a “rastreabilidade clínica” é difícil de ser alcançada visto a “complexidade físico-química” das amostras humanas, causada sobretudo pela variação biológica intraindividual e interindividual.⁽¹⁴⁾

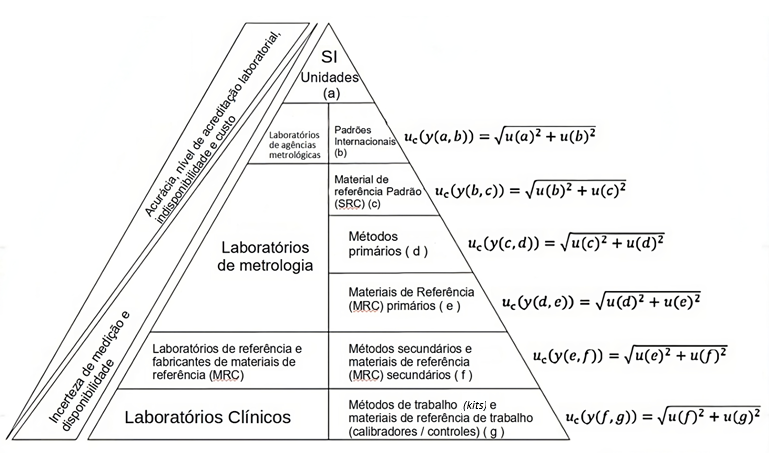
Figura 6

Cadeia de rastreabilidade metrológica envolvida na mensuração de resultados em exames de laboratórios clínicos.

Fonte: Adaptado de Pereira, 2016.⁽⁶⁾

 

Abordagem top-down para cálculo da incerteza de medição         

Ao longo do tempo em que a incerteza de medição foi estudada e suas implicações analíticas observadas, surgiram diferentes abordagens para determinação da incerteza de medição. A abordagem, conhecida atualmente como top-down, ou seja, de “cima pra baixo” busca a determinação da incerteza a partir de estimativas de precisão baseadas em estudos interlaboratoriais de avaliação do desempenho de métodos que possam representar a incerteza como um todo do processo de medição e foi proposta por Wernimont em sua publicação nos anos 1980.⁽¹⁵⁾ Esta abordagem foi retomada tempos depois, em 1995, pelo Comitê de Métodos Analíticos (AMC) da Sociedade Real de Química⁽¹⁶⁾ e pelo Comitê Nórdico para Análises de Alimentos (NMKL), que também sugeriu uma estratégia similar, mas tendo como base apenas dados provenientes de avaliações intralaboratoriais.^(10,14) Estas recomendações surgiram pelo fato que na abordagem Top-down, a maior parte dos dados necessários para a determinação da incerteza de medição, já estão disponíveis a partir dos resultados obtidos quando o método é validado, conforme as preconizações exigidas⁽¹⁷⁾, em contrapondo com a abordagem descrita e padronizada pelo GUM (Guide to the expression of Uncertainty in Measurement)⁽³⁾, publicada em 1993 pela ISO (International Standard Organizations), do tipo bottom-up, que necessita da identificação e quantificação das fontes de incerteza individuais que contribuem para a incerteza de medição, o que nem sempre é possível em laboratórios clínicos. Desta forma, na prática, a aplicação do modelo GUM não é diretamente possível em um significativo número de situações nos laboratórios clínicos.⁽¹¹⁾

Em laboratórios clínicos as ferramentas mais conhecidas de estatísticas relacionadas ao desempenho analítico são os resultados de imprecisão, avaliados em programas de CIQ ou de inexatidão, através de ferramentas de avaliação em relação às análises de amostras controle com valores preestabelecidos ou com médias de consenso como os ensaios de proficiência (EP), estes últimos responsáveis por nos apresentar o que conhecemos como “bias”, entre as estratégias de avaliação da qualidade.⁽¹⁰⁾ Rigo-Bonnin e colaboradores⁽¹⁸⁾ apresentaram, em 2018, um estudo em que compararam três estratégias diferentes, todas consideradas do tipo “top-down”, para estimar a MU de um método de UHPLC-MS/MS para quantificação de tacrolimus, um imunossupressor bastante utilizado na prática clínica. Foram utilizados como estratégias: 1. Dados de validação individual do laboratório, relativos à imprecisão, e dados de bias baseados na utilização de material de referência certificado (MRC) e adicionando a incerteza associada aos calibradores utilizados nos ensaios; 2. Dados relacionados à participação em programa de CIQ, com utilização de material de controle comercial (Liquicheck™ Whole Blood Immunosuppressant) e comparação de resultados em grupos interlaboratoriais (UNITY™ Interlaboratory Program); 3. Dados relacionados à participação em programa de CEQ do tipo EP “bias” (IPTS: Immunosuppressant Proficiency Testing Schemes – CITAC – Cyclosporin and Tacrolimus (LGC™ Standards)). As três estratégias obtiveram como valores de estimativa de MU 11,8%, 13,2% e 13,0%, respectivamente.⁽¹⁸⁾ Frenkel e colaboradores propuseram, em 2019, um algoritmo visando equalizar a utilização de “bias” de forma que se possa obter a incerteza padrão do “bias”, que como um erro observável em valores preestabelecidos pode incorporar também os erros randômicos e, desta forma, ser incorporadas na MU.⁽¹⁹⁾

Outro exemplo da aplicação deste tipo da abordagem foi descrito por Eren e Oguz,⁽²⁰⁾ em 2022, sobre a estimativa da incerteza de medição de uma análise disponível comercialmente para medida da hemoglobina glicada A1c no sistema analítico validado, Atellica (Siemens Healthineers, Alemanha).⁽²⁰⁾ Neste exemplo, utilizaram resultados de CIQ e CEQ, obtidos em um período de 6 meses, para calcular a MU, de acordo com o documento CLSI EP29-A⁽⁵⁾, utilizando a seguinte fórmula geral:

u_c = √(u_Rw²+u_bias²),

U = k × u_c,

onde U é a incerteza expandida e k é o fator de abrangência (para nível de confiança [IC] de 95%, k = 2,0), u_Rw é a incerteza padrão relativa devido à imprecisão intralaboratorial, associada a possíveis erros aleatórios e obtida pelo cálculo do coeficiente de variação (CV%) de dois níveis de materiais de controle de qualidade interno (CV₁% e CV₂%), obtida na seguinte fórmula:

 u_Rw = √[(CV₁ ² +CV₂ ² )/2].

Os resultados do controle de qualidade externo, de 6 meses, obtidos do programa controle externo da qualidade, EQAS da Bio-Rad^®, foram usados para calcular a incerteza do bias (u_bias) que aponta possíveis erros sistemáticos. O valor médio quadrático dos resultados mensais do bias do laboratório (RMS_bias) e a incerteza do valor de referência do programa EQAS (u_cref) foram calculados. Em seguida, a u_bias padrão foi calculada de acordo com a fórmula:

 u_bias = √ [(RMS_bias)² + (u_cref)²]

Considerando que

    RMS_bias = √ [(Σ_bias(CEQ)²/n],

na qual “n” é o número de rodadas no CEQ,

    u_cref=(sR/√n),

onde sR é o CV% médio do resultado do controle externo da qualidade e n é o número de grupos de pares que participam do programa EQAS.

A incerteza padrão combinada, u_c, foi quantificada na forma a seguir:

  u_c =√(u_Rw² + u_bias² ).

Por fim, considerando IC de 95%, temos que:

      U = 2,0  ×  u_c.

No estudo em questão, os valores de CV médios em dois níveis foram CV₁% = 3,16 e CV₂% = 2,79, que foram avaliados em relação à especificação da qualidade exigida pelo NGSP (National Glycohemoglobin Standardization Program), que preconiza imprecisão ≤4%. Consequentemente, a u_Rw% foi de 2,98. Os parâmetros relacionados ao bias apresentaram como valor RMS_bias% = 1,17 e u_cref% = 0,07. Desta forma, aplicando-se as fórmulas acima, temos que a incerteza combinada (u_c) foi de 3,2% e a incerteza expandida (U) foi de 6,4%. O valor de decisão, utilizado como critério diagnóstico de Diabetes mellitus (DM), é de 6,5% de HbA1c no total de HbA e aplicando-se a incerteza de medição expandida (U) obtida no cálculo, temos que: 6,5 x 0,064 = 0,416% ~ 0,4%. Desta forma, a expressão do resultado, considerando que o reporte da expressão dos resultados devem incluir a MU de forma clara⁽²¹⁾, preferencialmente na forma de “Resultado do exame ± MU” (seja como valor numérico na mesma unidade do mensurando, porcentagem ou range^(22,23) no ponto de decisão clínica seria:

  HbA1c: 6,5%±0,4 (Range: 6,1% a 6,9%).

Considerando o limite aceito de especificações da qualidade analítica para HbA1c como ±0,5%,⁽²⁴⁾ temos que a U obtida está em conformidade analítica. Portanto, o valor do resultado do mensurando é o valor médio dentro da faixa (range) das probabilidades de conter o valor verdadeiro.

 

Abordagem bottom-up (recomendada pelo GUM) para cálculo da incerteza de medição

A abordagem muito conhecida, e utilizada, sobretudo em processos de validação no desenvolvimento de métodos, em especial dos métodos “in house”, é a bottom-up, particularmente adotada pelo EURACHEM a partir dos anos 1990 como referência de uso na química analítica.⁽³⁾

Na abordagem bottom-up a incerteza de medição é calculada através de uma série de passos que envolvem a identificação e quantificação das fontes de incerteza:

1. Identificação das Fontes de Incerteza: Identificar todas as possíveis fontes de incerteza que podem afetar a medição. Isso pode incluir fatores como a precisão do instrumento de medição, as condições ambientais, o método de medição, entre outros.
2. Tipos de Incerteza: Existem dois tipos de incertezas, as do Tipo A e do Tipo B. As incertezas são de tipos diferentes porque são calculadas por procedimentos distintos, mas ambos são baseados em distribuição de probabilidade e os componentes de incerteza resultantes de cada tipo são quantificados por variância ou desvios padrão.^(3,6,11)

2.1       Incertezas do Tipo A: As incertezas de Tipo A são encontradas por meios estatísticos, sendo calculadas por meio do desvio padrão de várias medidas obtidas por meio de repetição. Visto que a melhor estimativa para o valor esperado é a média dos dados obtidos no processo, a incerteza será o desvio padrão da média. Além disso, é necessário avaliar quantos graus de liberdade devem ser indicados Também é importante ressaltar que, quando apropriado e uma vez identificadas, covariâncias também devem ser indicadas.^(6,11) Por exemplo, imagine um resultado médio de 31,7mg/dL de HDL-Colesterol, obtido após um conjunto de 10 determinações com coeficiente de variação igual a 2,9. Neste caso, o desvio padrão da média é aproximadamente 0,92. Esse dado reflete a incerteza do Tipo A associada a essas medidas, sendo um dos componentes da incerteza combinada.

2.2       Incertezas do Tipo B: As incertezas do Tipo B são encontradas de outras formas, já que não são calculadas por meios estatísticos, o que exige uma série de conhecimentos relacionados aos instrumentos e materiais envolvidos no processo. Essas informações são as especificações do fabricante, os certificados de calibração e outras especificidades e as incertezas que constam em manuais e outras referências.^(6,11)

3. Quantificação das Fontes de Incerteza: A quantificação de cada fonte de incerteza pode ser feita através de métodos estatísticos, como a análise de repetibilidade e reprodutibilidade, ou através de informações fornecidas pelos fabricantes dos instrumentos. Converter os valores de componentes de incerteza em valores de desvios padrão (DP) relativos ao mensurando.^(6,11)

3.1 Combinação das Incertezas: As incertezas individuais devem ser combinadas para obter a incerteza total. Isso geralmente é feito utilizando a fórmula da raiz quadrada da soma dos quadrados (RSS), que é uma forma de combinar incertezas independentes. Onde (u_c) é a incerteza combinada e ( u₁², u₂², …, u_n²) são as incertezas individuais. A relação geral entre a incerteza padrão combinada u_c(y) de um valor y e a incerteza dos parâmetros independentes X₁, X₂, …X_n dos quais depende é:^(6,11)

3.2 Expansão da Incerteza: Da mesma forma que na abordagem top-down, em muitos casos a incerteza combinada é multiplicada por um fator de abrangência (k) para obter a incerteza expandida, que fornece um intervalo de confiança maior. O valor de (k) é geralmente escolhido com base no nível de confiança desejado, por exemplo k = 2, para um nível de confiança de 95% (95% IC).

U = k × u_c

Onde (“U”) é a incerteza expandida.

Esses passos ajudam a garantir que a incerteza de medição seja bem compreendida e quantificada, permitindo uma melhor interpretação dos resultados de medição.^(6,11)

 

Influência da incerteza de medição na prática laboratorial e clínica

A MU pode ter impactos significativos nos resultados práticos, influenciando a interpretação e a confiabilidade dos dados obtidos, sobretudo se não for levada em consideração ou se os profissionais responsáveis pelas interpretações dos resultados dos exames laboratoriais não estiverem devidamente familiarizados com este conceito.⁽⁶⁾ Especialmente importante é o conhecimento sobre as estimativas de MU quando um valor de mensurando estiver próximo a uma linha de corte definida por diretriz ou consenso médico, para tomada de decisão clínica, como estabelecer um diagnóstico de uma condição de saúde ou doença. O exemplo abordado anteriormente, do valor de 6,5% de HbA1c como critério de decisão para diagnóstico de DM⁽²⁴⁾ ilustra bem a questão. Um hipotético resultado de HbA1c que esteja ligeiramente acima do valor definido como mínimo para estabelecer o diagnóstico de DM, como 6,7% por exemplo, tendo a MU do método utilizado sido estimada em ±0,4%, efetivamente seria de 6,7%±0,4%. Este resultado, portanto, não reúne condições estatísticas e metrológicas necessárias para embasar a tomada de decisão clínica satisfatoriamente, considerando que o valor verdadeiro da medição pode estar abaixo de 6,5%,⁽²⁴⁾ de forma que para o diagnóstico de DM sejam levados em consideração os resultados de outros exames laboratoriais e a sintomatologia envolvida.

Neste contexto, o suplemento 6 do GUM, traduzido pelo INMETRO em 2022 e denominado “Avaliação de dados de medição – O papel da incerteza de medição na avaliação da conformidade”⁽²⁵⁾, fornece uma série de critérios e subsídios referentes à avaliação de conformidade de um resultado frente ao seu propósito esperado, como limites e intervalos de tolerância, probabilidade de conformidade, intervalos de aceitação, riscos ao consumidor/cliente. Também o documento CLSI EP29-4 estabelece critérios e diretrizes para a MU e sua expressão nos resultados de laboratórios clínicos.⁽⁵⁾

As informações necessárias para relatar o resultado de uma medição variam conforme o uso pretendido. Em um laboratório clínico, o consumidor final é o paciente ou um doador de sangue, que não é responsável pelo seu próprio diagnóstico ou monitoramento. O principal cliente, neste caso, é o médico ou outro profissional responsável pela ação técnica, como triagem, diagnóstico ou acompanhamento.⁽⁶⁾ O profissional que toma decisões com base nos resultados laboratoriais deve compreender o propósito e o valor da MU para o julgamento. Caso contrário, os relatórios de incerteza de medição podem gerar dúvidas que comprometam a decisão clínica. Essas habilidades são raras entre médicos e outros profissionais de saúde, que geralmente não solicitam essa informação por não entenderem seu conceito e, por este motivo, a maioria dos laboratórios clínicos, sobretudo os hospitalares, não relata a incerteza de medição, pois ela pode não agregar valor à maioria das decisões clínicas e pode atrapalhar ao causar indecisão na interpretação, sobretudo em resultados de exames de urgência.⁽⁶⁾

Em resumo, a MU é um fator crítico que deve ser gerenciado cuidadosamente para garantir que os resultados sejam confiáveis e úteis para a aplicação prática desejada, pois afeta diretamente a confiabilidade e a validade dos resultados obtidos.⁽⁷⁾ A MU fornece uma indicação quantitativa da qualidade dos resultados, uma vez que são características inversamente proporcionais.⁽²⁵⁾ A ausência desta informação dificulta avaliar a precisão e a exatidão dos resultados, embora existam legislações e programas de qualidade a serem seguidos pelos laboratórios clínicos. Consequentemente, muitos médicos acabam avaliando a qualidade dos resultados de forma empírica e subjetiva, muitas vezes sem base em evidências ou estatísticas por desconhecerem estes conceitos. Ignorar ou subestimar a incerteza de medição pode levar a erros significativos, afetando a qualidade do processo de medição e, consequentemente, a segurança do paciente.⁽⁷⁾

 

CONSIDERAÇÕES FINAIS

A estimativa e a quantificação da incerteza de medição são fundamentais na prática laboratorial e clínica, pois garantem a precisão e a confiabilidade dos resultados dos exames diagnósticos. Compreender a incerteza é essencial para a interpretação adequada dos resultados, especialmente em contextos críticos como o diagnóstico de doenças, em que pequenos desvios podem levar a decisões clínicas erradas. As abordagens top-down e bottom-up fornecem estratégias complementares para a determinação da incerteza, cada uma com suas aplicações específicas no ambiente clínico. Apesar das diretrizes e normas que regulam a prática laboratorial, a falta de familiaridade dos profissionais de saúde com o conceito de incerteza pode comprometer a eficácia do diagnóstico e o manejo do paciente. Os laboratórios clínicos podem efetuar as estimativas de MU por meio de planilhas eletrônicas utilizando abordagens variadas, conforme descrito neste artigo, inclusive adotando mais de uma abordagem de forma complementar, como análise da reprodutibilidade e “bias” em conjunto, através de um conjunto de dados de CIQ e CEQ, como a participação em EP. Porém, a incorporação de softwares e programas de controle da qualidade interlaboratoriais, que permitam automatizar o processo de estimativa da MU (como Bio-Rad UNITY™,⁽²⁶⁾ Randox Acusera 24/7™⁽²⁷⁾ e Controllab CI ONLINE™⁽²⁸⁾), pode contribuir, de forma decisiva, para a incorporação deste conceito na prática laboratorial e clínica. Portanto, é imperativo que a comunidade médica reconheça a importância da incerteza de medição e trabalhe para integrá-la nas decisões clínicas, promovendo assim um atendimento mais seguro e eficaz. O futuro da medicina laboratorial dependerá de uma abordagem mais holística, em que a qualidade dos resultados, incluindo suas incertezas, seja considerada uma prioridade na prestação de cuidados de saúde.

 

 

REFERÊNCIAS

1. Vocabulário Internacional de Metrologia: Conceitos fundamentais e gerais e termos associados (VIM 2012). Duque de Caxias, RJ. 2012. 94p. Disponível em: <http://www.inmetro.gov.br/inovacao/publicacoes/vim_2012.pdf>. Acesso em: 21 ago. 2024.
2. Ćelap I, et al. Measurement uncertainty estimation recommendations. Biochemia medica (Zagreb) 2017;27(3):030502. Disponível em: <https://doi.org/10.11613/BM.2017.030502>. Acesso em: 14 ago. 2024.
3. EUROCHEM / CITAC (2012). Quantifying uncertainty in analytical measurement – QUAM:2012.P1, Guide CG4, 3nd ed. 2012. Disponível em: <https://eurachem.org/images/stories/Guides/pdf/QUAM2012_P1.pdf>. Acesso em: 21 ago. 2024.
4. ACC Engenharia de medição. Processo de medição: entenda seu impacto nos processos e produtos! Disponível em: <https://accmetrologia.com.br/backup-plim/processo-de-medicao-entenda-seu-impacto-nos-processos-e-produtos/>. Acesso em: 18 ago. 2024.
5. CLSI EP29-A – Expression of Measurement Uncertainty in Laboratory Medicine; Approved Guideline. 32, Nº 4, 2012. Disponível em: <https://clsi.org/standards/products/method-evaluation/documents/ep29/>. Acesso em: 21 ago. 2024.
6. Pereira P. Uncertainty of Measurement in Medical Laboratories. DOI: 10.5772/62437. In book: New Trends and Developments in Metrology (pp.51-80). Publisher: InTech, Editors: Luigi Cocco, (2016). Disponível em: <https://www.researchgate.net/publication/303289783_Uncertainty_of_Measurement_in_Medical_Laboratories>. Acesso em: 18 ago. 2024.
7. Fernandes JLN, Wollinger W, Garrido BC. Rastreabilidade em medicina laboratorial: um estímulo global para resultados exatos no cuidado com o paciente. Jornal brasileiro de Patologia e Medicina Laboratorial, v. 55, n. 4, p. 402–411, 2019. Disponível em: <https://www.scielo.br/j/jbpml/a/5DrKpSwPrM93mcmNNp7Fkqw/>. Acesso em: 20 ago. 2024.
8. Belk WP, Sunderman FW. A survey of the accuracy of chemical analyses in clinical laboratories. American Journal of Clinical Pathology, v. 17, n. 11, p. 853–861, 1947. Disponível em: <https://academic.oup.com/ajcp/article-abstract/17/11/853/1761299?redirectedFrom=fulltext>. Acesso em: 20 ago. 2024.
9. Ricós C, et al. Current databases on biological variation: pros, cons and progress. Scandinavian Journal of Clinical and Laboratory Investigation, v. 59, n. 7, p. 491–500, 1999. Disponível em: <https://pubmed.ncbi.nlm.nih.gov/10667686/>. Acesso em: 21 ago. 2024.
10. Kallner A. Estimation of uncertainty in measurements in the clinical laboratory. Clinical chemistry and laboratory medicine 2013; 51(12): 2249–2251. DOI 10.1515/cclm-2013-0749. Disponível em: <https://www.degruyter.com/document/doi/10.1515/cclm-2013-0749/html>. Acesso em: 18 ago. 2024.
11. Milinkovic, et al.: Uncertainty of measurement in laboratory medicine. Journal of Medical Biochemistry 2018; 37 (3). DOI: 10.2478/jomb-2018-0002. Disponível em: <https://pubmed.ncbi.nlm.nih.gov/30584397/>. Acesso em: 18 ago. 2024.
12. Disponível em: <https://towardsdatascience.com/understanding-the-68-95-99-7-rule-for-a-normal-distribution-b7b7cbf760c2>. Acesso em: 10 ago. 2024.
13. Junior E. Desvendando o Teorema Central do Limite. Disponível em: <https://medium.com/data-hackers/desvendando-o-teorema-central-do-limite-17cbb13beb1a>. Acesso em: 19 set. 2024.
14. Milinković N, Jovičić S, Ignjatović S. Measurement uncertainty as a universal concept: can it be universally applicable in routine laboratory practice? Critical reviews in clinical laboratory sciences, v. 58, n. 2, p. 101–112, 2021. Disponível em: <https://pubmed.ncbi.nlm.nih.gov/32672116/>. Acesso em: 21 ago. 2024.
15. Wernimont GT. Use of statistics to develop and evaluate analytical methods, AOAC: Arlington, 1985.
16. Royal Society of Chemistry / Analytical Methods Committee. Uncertainty of measurement: implications of its use in analytical science Analyst 1995, v. 120, p. 2303-2308.
17. de Oliveira EC, de Aguiar PF. Comparação de diferentes abordagens para avaliação da incerteza Química nova, 32, n. 6, 2009. Disponível em: <https://doi.org/10.1590/S0100-40422009000600051>. Acesso em: 18 ago. 2024.
18. Rigo-Bonnin R, et al. Different top-down approaches to estimate measurement uncertainty of Whole blood tracolimus mass concentration values. Clinical biochemistry 57 (2018) 56-61. Disponível em: <https://doi.org/10.1016/j.clinbiochem.2018.05.005>. Acesso em: 21 ago. 2024.
19. Frenkel R, Farrance I, Badrick T. Bias in analytical chemistry: A review of selected procedures for incorporating uncorrected bias into the expanded uncertainty of analytical measurements and a graphical method for evaluating the concordance of reference and test procedures. Clinica chimica acta; international journal of clinical chemistry, v. 495, p. 129–138, 2019. Disponível em: <https://www.sciencedirect.com/science/article/abs/pii/S0009898119317383?via%3Dihub>. Acesso em: 21 ago. 2024.
20. Eren F, Oguz, EF. The estimation of measurement uncertainty of glycated hemoglobin at atellica solutions. International Journal of Medical Biochemistry, 2021.. DOI: 10.14744/ijmb.2021.84755. Disponível em: <https://internationalbiochemistry.com/jvi.aspx?un=IJMB-84755&volume=>. Acesso em: 21 ago. 2024.
21. ISO 15189-2012 Medical laboratories – Requirements for quality and competence. International Organization for Standardization, 2012.
22. Coskun A, Berçik İnal B, Serdar M. Measurement uncertainty in laboratory medicine: the bridge between medical and industrial metrology. Turkish journal of biochemistry, v. 44, n. 2, p. 121–125, 2019. Disponível em: <https://www.degruyter.com/document/doi/10.1515/tjb-2019-0170/html>. Acesso em: 20 ago. 2024.
23. Plebani M, et al. What information on measurement uncertainty should be communicated to clinicians, and how? Clinical biochemistry, v. 57, p. 18–22, 2018. Disponível em: <https://www.sciencedirect.com/science/article/abs/pii/S0009912017311803?via%3Dihub>. Acesso em: 18 ago. 2024.
24. Galindo-Méndez M, Sánchez-López A, Cruz-Fuentes L. The estimation of uncertainty of measurement of glycated hemoglobin as an analytical performance specification and in the interpretation of its results. Clinical biochemistry, v. 63, p. 92–96, 2019. Disponível em: <https://www.sciencedirect.com/science/article/abs/pii/S0009912018309263?via%3Dihub>. Acesso em: 20 ago. 2024.
25. INMETRO – JCGM 106:2012. Avaliação de dados de medição — Suplemento 6 do “Guia para a expressão de incerteza de medição” — O papel da incerteza de medição na avaliação da conformidade. Duque de Caxias, RJ: INMETRO/CICMA/SEPIN, 2022.
26. Bio-Rad UNITY Quality control data management. Disponível em: <https://www.bio-rad.com/pt-br/applications/quality-management/data-management-systems>. Acesso em: 18 set. 2024.
27. Randox Acusera 24/7 – Measurement Uncertainty Vs Total Error. Disponível em: <https://www.randox.com/mu-vs-te/>. Acesso em: 18 set. 2024.
28. Controllab CI ONLINE. Disponível em: <https://controllab.com/solucoes/controle-interno/>. Acesso em: 18 set. 2024.

 

Correspondência

José Robson Venturim

E-mail: [email protected]